İnsanın Ufkunu Açan En Önemli Şeyin Matematik Olduğunu Kanıtlayan Formüller ve Sonuçları
Matematik.
Evren hakkında bilgi sahibi olmamızı sağlayan, evreni günden güne daha çok tanımamıza vesile olan bir bilim dalı.
Matematik.
Not: Ekşi Sözlük yazarı elma alan satan aç maymun'un yazısından alıntıdır
Pi (π) Sayısı
Temelleri Arşimet tarafından atılan ve günümüzde yaklaşık 3 trilyon basamağına kadar gidebildiğimiz irrasyonel sayı. Sayı, birçok filozof tarafından mükemmel şekil olarak kabul edilen çemberin çevresinin çapına oranına eşit.
Pi bir dairenin çevresinin çapına oranıdır. Hala sınırları bilinmediğinden kesirli hiçbir sayıyla tam olarak ifade edilemez. (22/7 gibi)
Aklımızın bir köşesine bunu yazalım şimdi..
e Sayısı
John Napier tarafından keşfedilmek üzere olan, Jacob Bernoulli tarafından keşfedilen ve Leonhard Euler tarafından ismi konan bir irrasyonel sayı.
Sayının bulunuş hikayesi bileşik faize dayanıyor. Hikayemiz paraya doymayan bir adam hakkında. Elinde 1 lirası olan bir adam eğer bu parasını yıllık %100 faizle bir yıllığına faize yatırırsa sene sonunda parası 2 lira olur. Gayet güzel para. Ancak bu adam 2 lira ile yetinmeyip parasını 6 ayda bir %50 faizle 1 yıl yatırırsa sene sonunca parası 2.25 lira olur. Bu durumu fark eden çakal adam, parasını 3 ayda bir %25 faizle 1 yıl yatırırsa sene sonunda parası 2.4414 lira olur.
Yani faiz oranı küçülüp aynı oranda faizin işleme frekansı arttıkça adamın yıl sonundaki parası artar.
Adamın yatırdığı para = 1
Adamın yıl sonundaki parası = y
Faiz oranı = 1/x
Faiz frekansı = x
olarak düşünülürse;
bizim elemanın yıl sonundaki parası y = (1+1/x)^x olacaktır. Bu artan para, hesaplarımızdan da görüldüğü üzere azalarak artan bir grafik çizer ve bir değere çok yaklaşır. Sonsuza giden grafiklerin hangi değere yaklaştığını bulmamıza yarayan limit, bu değeri bulmak için de bize yardım eder.
lim x->sonsuz (1+1/x)^x değeri sizin de tahmin edebileceğiniz gibi e sayısı.
Bu eşsiz sayıyla ilgili meşhur bir örnek de şudur:
Bir restorana giren müşteriler şapkalarını vestiyere bırakır ancak şapkaları numaralandırmayı unutan adam restorandan çıkan her müşteriye rastgele bir şapka verir. Müşteri sayısı arttıkça müşterilerin hepsine yanlış şapkayı verme olasılığı da 1/e'ye yaklaşır.
Ayrıca bu e sayısının x. kuvveti, türevi kendisine eşit olan yegane sayıdır.
Bu sayıyı ve hikayesini de atıyoruz hafızaya..
i Sayısı
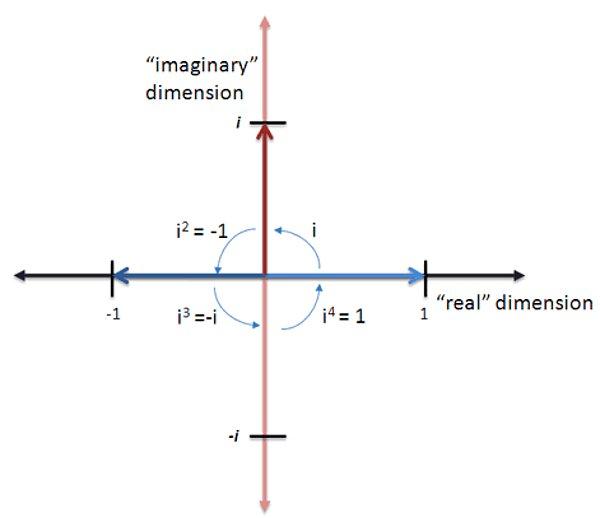
Bilim adamlarına ve yaptıkları deneylere göre evrendeki her şeyin bir de karşıt değeri yani onu 0'a tamamlayan bir tersi vardır. Bu temel kuralın benzeri matematikte de uygulanabilir. Örneğin bir sayıyı bir sayıyla çarpabiliyorsak bu sayıları birbirine bölebiliriz de. Bir sayının karesini alabiliyorsak bir sayının karekökünü de alabiliriz gibi.
0'dan büyük sayıların karelerini ve kareköklerini almak kolay ancak 0'dan sola doğru gidince bu iş karmaşıklaşıyor. -1'in karesini alıyoruz ancak karekökü hakkında bir şey söyleyemiyoruz. Söylememiz gerek diyen matematikçiler de demiş ki madem reel bir kökü yok bu -1'in demek ki bizim bilmediğimiz bir sayı kümesinde kökü var. İşte bu sayı kümesine de sanal sayılar demişler ve ilk tam sayısına da; kurgusal, hayali anlamına gelen latince kelime imaginarius'un baş harfi olan i'yi layık görmüşler.
Bu 3 Sayının Mükemmel Eşitliği
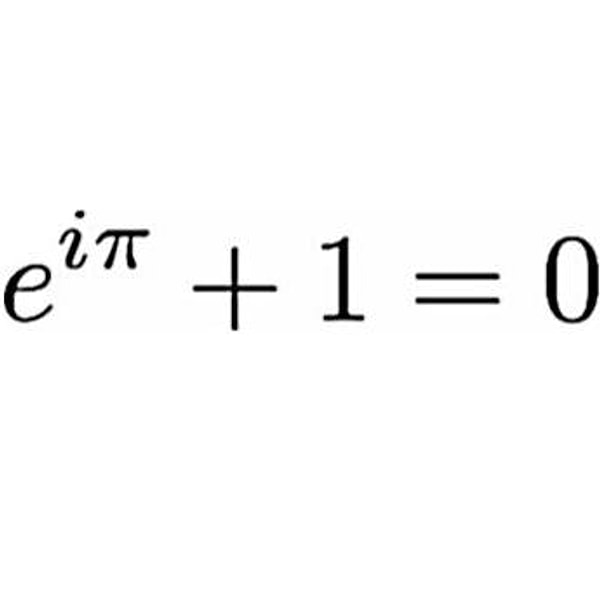
Bileşik faizden bulduğumuz eşsiz sayının üzerine mükemmel şekilden elde ettiğimiz sayı ve reel sayı kümesine dik bir hayali sayı kümesinde bulunan sayının çarpımını yazınca sonuç -1 oluyor. Bu denklemin adı ise Euler özdeşliği. Euler özdeşliği ile ilgili en önemli ve kayda değer bilgiler ise aşağıda:
Mathematical Intelligencer okurları tarafından yanıtlanan bir anket sonucuna göre euler özdeşliği matematiğin en hoş kuramıdır. Physics World tarafından 2004 yılında yapılan bir diğer anket sonucuna göre ise Euler eşitliği Maxwell denklemleri ile birlikte 'gelmiş geçmiş en büyük denklemler' olarak belirlenmiştir.
Paul Nahin'in Dr. Euler'in enfes formülü (2006) adlı kitabı Euler özdeşliğine adanmıştır. Dört yüz sayfa uzunluğundaki bu kitap Euler özdeşliğinin 'matematiksel güzelliğin zirvesine ulaştığı' kanısındadır.
Constance Reid, Euler özdeşliğinin 'matematiğin en önemli formülü' olduğunu öne sürmüştür.
Gauss'un bu formülü ilk duyduğunda anlayamayan hiçbir öğrencinin birinci sınıf bir matematikçi olamayacağını söylediğine inanılmaktadır.
19. yüzyılın ünlü matematikçilerinden Benjamin Peirce bir dersinde özdeşliği kanıtladıktan sonra şunları söylemiştir: 'Bu özdeşlik ilk bakışta çelişkili gibi duruyor ancak bunu kanıtladıktan sonra gerçeğin ta kendisiyle karşı karşıya olduğumuzu görüyoruz.'
Stanfordlu matematik profesörü Keith Devlin, Euler özdeşliği hakkında şunları söylemiştir: 'Euler özdeşliği aşkın gerçek anlamını kavrayan bir Shakespeare sonatı ya da insanın ruhuna işleyen bir resim gibi varoluşun en derinlerine iniyor.'
Rosetta'nın Yolculuğu
Sonuç olarak sınavda sorulan zor sorular yüzünden Arşimet, Euler, Bernoulli gibi büyük adamlara küfretmeyin, matematiğe de sırf siz beceremiyorsunuz diye laf etmeyin.
'Bu kadar formüle ne gerek vardı abi' diyenlerin bu görsele tekrar tekrar bakmalarını özellikle öneriyorum..
Keşfet ile ziyaret ettiğin tüm kategorileri tek akışta gör!

